Stephen Griffies

Stephen Griffies

Ocean physicist

Philosophy + Aims

Ocean models provide a repository for mechanistic theories of how the ocean works, with numerical methods used to transform our mathematical physics theories into computational tools for scientific investigations. Mathematical physics theories and numerical methods provide the foundation for ocean models. The practice of ocean modeling uses numerical models as an experimental tool to help reveal mechanisms for patterns of ocean phenomena emerging from the governing equations (e.g., waves, instabilities, turbulence, jets, boundary currents, overturning circulation). Models and modeling form the two pillars of numerical and theoretical oceanography, with these pillars supported by, and in turn supporting, observational oceanography and laboratory studies.

Throughout my career I have endeavored to bring rigor and synthesis to the many intellectual strands comprising the foundations of ocean models and forming the practice of ocean modeling. This work has spanned nearly all areas of ocean and climate science, from ocean model algorithms and code development, climate model development, theoretical studies into subgrid scale parameterizations, and formulations of experimental protocols supporting the systematic analysis of model intercomparison projects. This page summarizes some of this work, and offers pointers for where research can bring further insights.

Science of Models

The science going into ocean models includes theories for how the ocean works (e.g., the equations of motion including subgrid scale parameterizations) and numerical methods for discretizing the mathematical equations. This section outlines areas where I have contributed to this science.

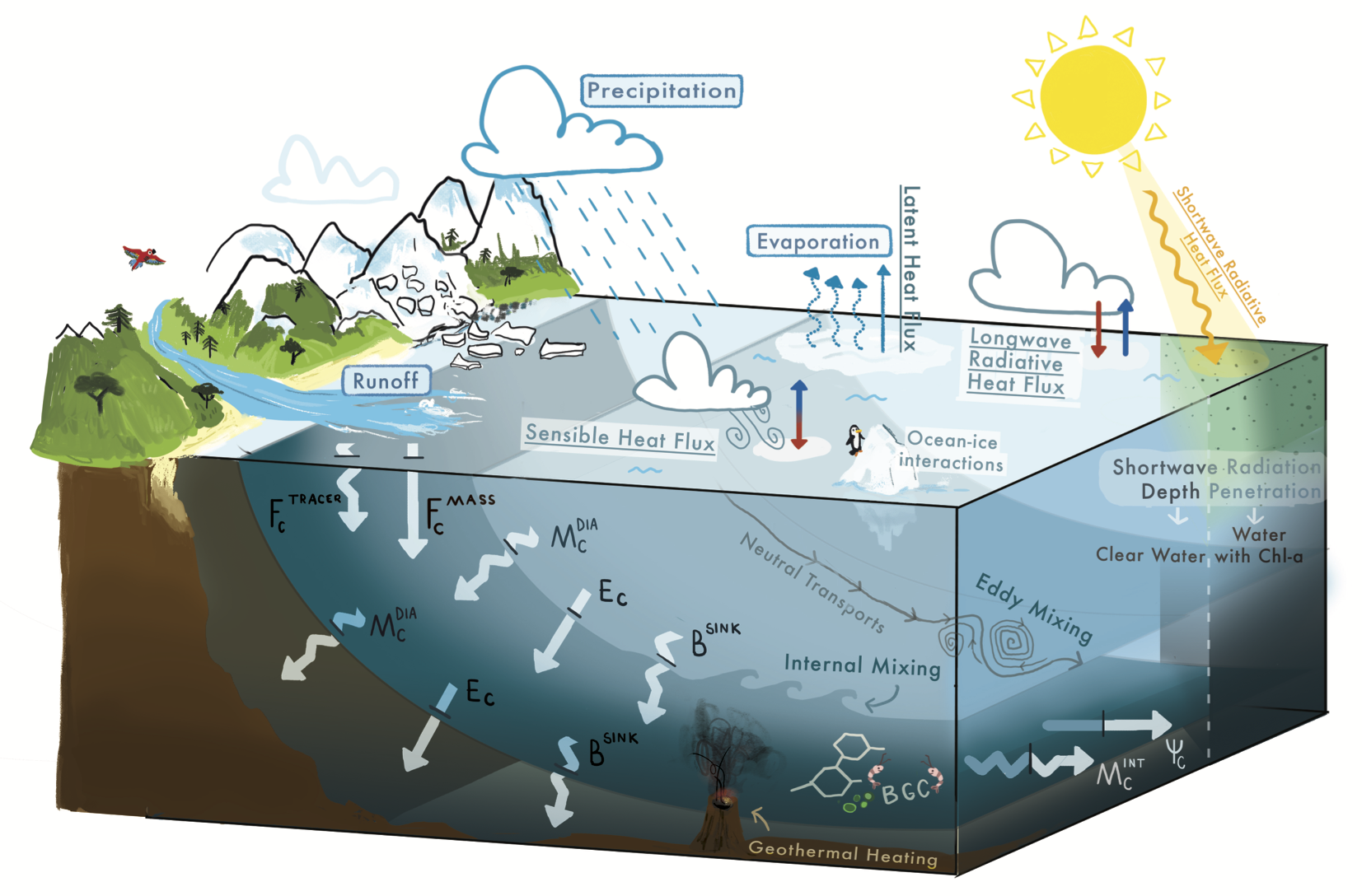
Schematic of processes that modify the ocean buoyancy or tracer concentration. Red (blue) surface arrows indicate heating (cooling). Changes in the tracer budget due to mass or tracer fluxes are indicated by straight and wiggly white arrows, respectively. This figure is from Groeskamp et al (2019), who synthesized concepts and methods of use to quantify how watermasses are transformed by physical and biogeochemical processes.

Model Foundations

As part of my work on ocean models foundations, I have offered both novel ideas and syntheses across a number of methods. Here are samples from this work.

Parameterizations

Drawing from Leonardo da Vinci of a turbulent flow. Notice the whirling vorticies breaking off from the eddying motion. Although the flow captured here has more connection to engineering applications, many of the ideas of 3d turbulence appropriate for this flow also apply to the turbulent boundary layers in the ocean, such as that discussed in Van Roekel et al (2018).

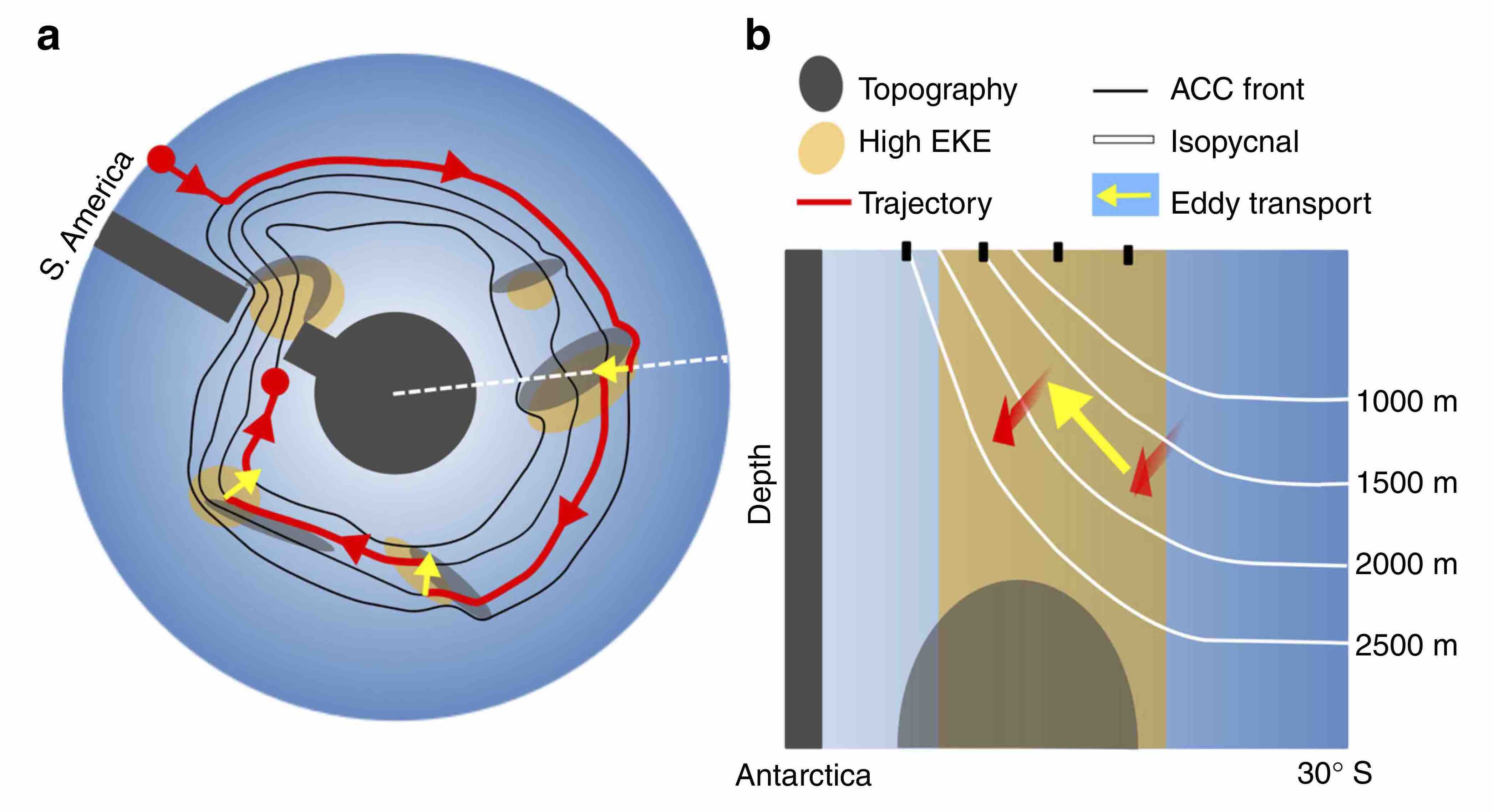
The ocean eddy parameterization problem is part of the larger turbulence closure problem, and it is among the most important and intellectually challenging problem in theoretical physical oceanography. It is important since eddy parameterizations, from the planetary boundary layer to the ocean interior to the bottom boundary layer, have a huge role in determining the performance of ocean climate models. It is challenging since it draws upon a wide variety of physical and mathematical skills. I have an ongoing interest in ocean eddy parameterization questions, and am particularly motivated by some exciting theoretical/modeling and observational studies conducted during recent years. This interest has led me to play a role in the NSF/NOAA funded Climate Process Team on ocean transport and eddy energy. Notably, there are many unsolved questions looking for energetic students and postdocs to help unravel!

Modular Ocean Model (MOM)

During the years 1997-2013, much of my working day consisted of developing MOM versions 3,4, and 5 (see this document for a brief history of MOM). This work was among the most rewarding of my career. Although I stopped focusing on development after MOM5 in early 2013, I remain engaged in a variety of scientific activities that make use of this code, most notably the COSIMA (Consortium for Ocean-Sea Ice Modelling in Australia) and the CM2.6 project. Both projects pursue studies of global climate at model resolutions that admit a rich field of mesoscale eddies.

More recent efforts of ocean code development at GFDL center on MOM6, which is a project led by my colleagues and friends Alistair Adcroft and Robert Hallberg. My focus on MOM6 has been on its diagnostic/analysis capabilities, with ongoing work aiming to make MOM6 as friendly to ocean analysts as it is to algorithm developers. Quite generally, MOM6 offers many sophisticated numerical features and physical parameterizations well beyond MOM5. These enhancements provide ocean modelers with critical tools needed to address a number of high profile climate related questions such as sea level rise and ocean heat uptake. My recent mentoring activities involve the use of MOM6 as a tool for idealized and realistic model simulations and analysis.

GFDL/Princeton leads on the MOM6 Project: Stephen Griffies, Robert Hallberg, Sonya Legg, and Alistair Adcroft in 2019.

Science of Modeling

When handed a numerical model, the scientist must decide how to use it for revealing phenomena (e.g., waves, turbulence, boundary currents, overturning circulations, climate variations) emerging from the fundamental equations. Questions arise surrounding how to design a numerical experiment that is reproducible by others who may wish to compare/contrast their model results. And when simulation results are obtained, questions then arise concerning how to rationalize the output through analysis and interpretation. Here I summarize areas where my research efforts have contributed to help answer these questions.

CORE/OMIP

Global ocean/sea-ice models are commonly used to help understand the mechanics of ocean climate variations and to directly compare to observations. In the absence of an interactive atmospheric model, the modeler must make decisions for how to force the ocean/sea-ice model in a way that does not compromise on the scientific investigation.

During the period from 2000 to 2009, I worked with colleagues on the CLIVAR Working Group for Ocean Model Development, now called the Ocean Model Development Panel (OMDP), to develop an experimental protocol for running global ocean/sea-ice models. This protocol is known as the Coordinated Ocean-sea ice Reference Experiments (CORE). The CORE protocol has become a community standard, thus forming the basis for the Ocean Model Intercomparison Project (OMIP) ongoing as part of CMIP6.

  • Coordinated Ocean-ice Reference Experiments (COREs): Griffies et al (2009)
  • OMIP contribution to CMIP6: experimental and diagnostic protocol for the physical component of the Ocean Model Intercomparison Project: Griffies et al (2016)

Analysis methods

Illustrating the pathways for fluid parcels to move both horizontally and vertically/meridionally within the Southern Ocean. This image is based on Lagrangian particle diagnostics as detailed in Tamsitt et al (2017) (see here for discussion of Southern Ocean research. Details of the Lagrangian diagnostic method are discussed in van Sebille et al (2018).

Given a robust model, a sensible experimental design, and sufficient computing, one then moves onto questions about how to rationalize the output from the simulation. This task brings us back to fundamentals, with the associated analysis confronting us with very basic questions about the underlying fluid mechanics. Here are some papers that develop a suite of analysis methods, some of which are of use for analyzing data from both models and observations.